New Journal Paper Out!

Weakly Supervised Learning (WSL) is currently an active research area, which aims to address challenges related to the available training data. According to Zhou, 2018 , WSL can be categorized into three types of approaches: (1) inexact supervision is related to the type of information being provided to the learning model, which it is not as accurate as necessary for it to work correctly. A more practical example of this scenario would be the use of data in the training step with coarse-grained information (e.g., cars and horses) and in the test step the model needs to classify new data from fine-grained classes (different car brands - Toyota and Peugeot); (2) inaccurate supervision, in the training data, some of the its labels may contain errors (noisy label). A common scenario in this supervision is learning from noisy labeled collections and trying to find the noisy labels to improve the results of the task in the target application; and (3) incomplete supervision, in a training set only a small amount of data has its labels provided, which is insufficient to obtain a good trained model. While another large part of the available data is unlabeled (unlabeled data). The focus of this paper is incomplete supervision, where only a small set of reliable training data is available, but other larger amounts of data remain unlabeled.

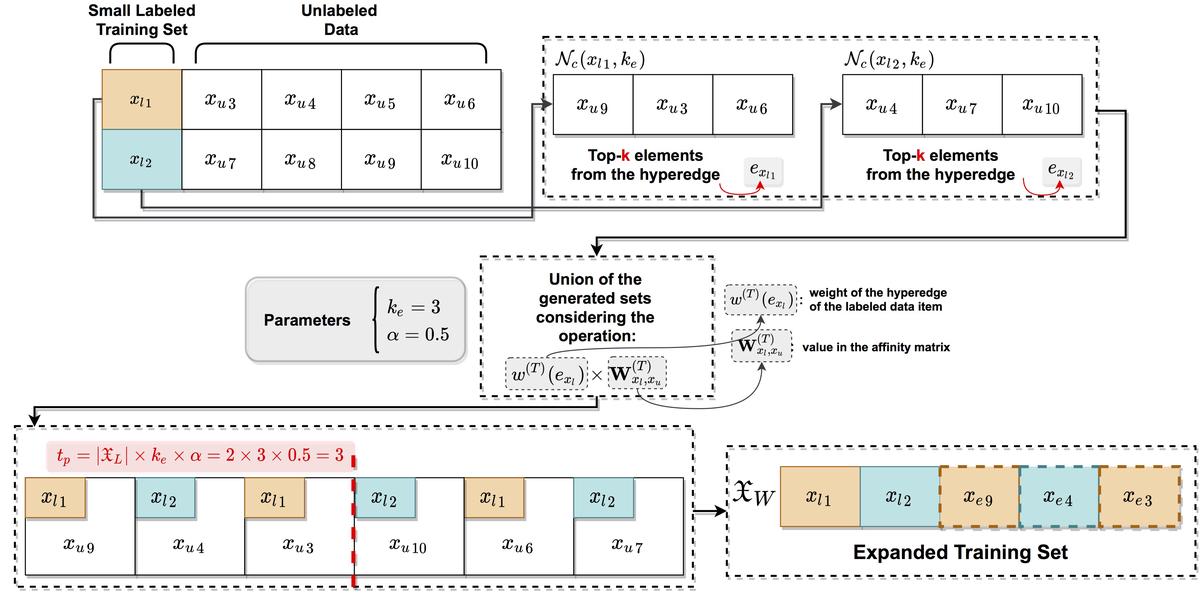
In this paper, we propose a novel weakly supervised approach for classification scenarios where only small labeled sets are available. The proposed method exploits an unsupervised manifold ranking algorithm based on hypergraphs (Pedronette et al., 2019) for labeled set expansion. Hypergraphs are a powerful generalization of graphs, i.e., while edges represent links between pairs of vertices, hyperedges allow representing relationships among a set of vertices (Bretto, 2013; Zhou et al., 2006). The proposed approach exploits hypergraph structures based on ranking information to identify and select reliable similarity relations between pairs of labeled-unlabeled data. Such relationships are exploited to compute an expanded labeled set used by supervised and semi-supervised classifiers.

The above figure illustrates how the hypergraph based expansion is performed. Starting with a small labeled set, we generate sets of unlabeled candidates $\mathcal{N}_c(x_q,k_e)$ containing the highest scores in the hyperedges $e_{x_{l}}$ (labeled items). In this example, we create sets based on the labeled data items $x_{l_{1}}$ and $x_{l_{2}}$ with the $k_{e}=3$ highest scores in their respective hyperedges. This creates a set of candidate pairs $\mathcal{C}$ that will be used to generate a rank $\tau_{\mathcal{C}}$ considering information in both hyperedges and the similarity matrix $\mathbf{W}$. Next, we select the candidate pairs of the previously generated rank $\tau_{\mathcal{C}}$ at the threshold position $t_{p}$. Considering the parameters specified in this example (i.e., $k_{e}=3$, $\alpha=0.5$, and $|\mathfrak{X}_{L}|=2$), we have $t_{p} = 3$. The last step of the method is to estimate the class of each entry of $\tau_{\mathcal{C}}$, which will be the class of the labeled data item that generated that entry. For instance, the unlabeled data item $x_{u_9}$ has the class of the labeled data item $x_{l_1}$ estimated, and so on. Furthermore, we remove any entries with different labeled data items associated, i.e., we do not label the same data item with different classes. Last but not least, an expanded labeled set $\mathfrak{X}_W$ is created, which then can be used to train a supervised or semi-supervised classifier.

Do you want to know more about achieving high accuracy results when only small labeled sets are available? Check our paper!